Теорема, обратная теореме о касательной к окружности: различия между версиями
Перейти к навигации
Перейти к поиску
(Новая страница: «Файл:3 обратная касательная.jpg») |
|||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
| + | ==Формулировка== | ||
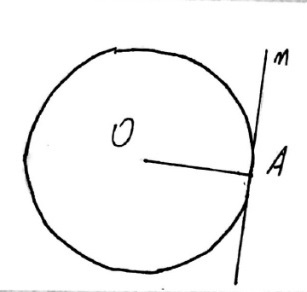
| + | ''Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.'' | ||
| + | |||
| + | |||
[[Файл:3 обратная касательная.jpg]] | [[Файл:3 обратная касательная.jpg]] | ||
| + | |||
| + | |||
| + | ==Доказательство== | ||
| + | |||
| + | ОА ⊥ р ⇒ расстояние от центра окружности до m - r∃ (∙) Н ∈ m: ОН⊥m | ||
| + | ⇒ m и окружность имеют одну общую точку | ||
| + | ⇒ m - касательная | ||
| + | '''ч.т.д.''' | ||