Свойство параллелограмма ( противоположные углы ): различия между версиями

Текущая версия на 18:11, 12 января 2020

1. ABCD - параллелограмм, значит AB = CD, BC = AD

2. Треуг. ABC = треуг. ACD по 3м сторонам ( AB=CD, BC = AD, AC-общая)

3. Значит $\angle 1$ и $\angle 3$ равны

4 Треуг. ABD = треуг. BCD по 3м сторонам ( AB=CD, BC = AD, BD-общая)

5. Значит $\angle 2$ и $\angle 4$ равны , ч.т.д.

@@ Строка 3: / Строка 3: @@
 [[Файл:Св-ва параллелограмма ( прот. углы).jpg ]]
+==Доказательство==
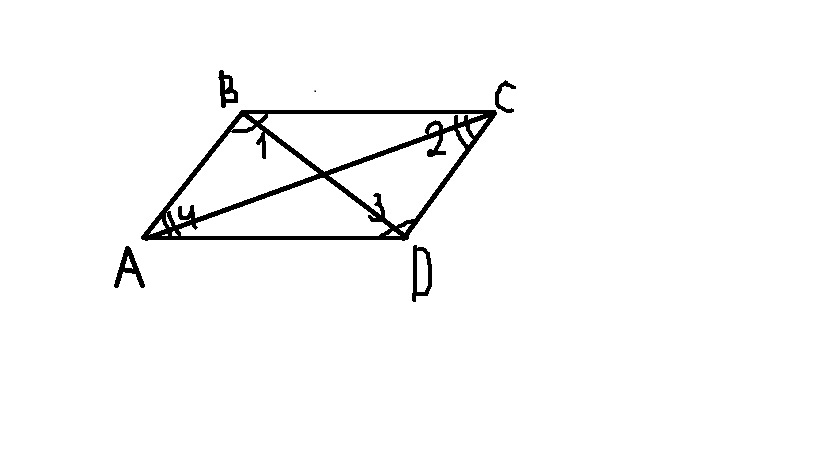
+. ABCD - параллелограмм, значит AB = CD, BC = AD
+. Треуг. ABC = треуг. ACD по 3м сторонам ( AB=CD, BC = AD, AC-общая)
+. Значит  <math>\angle 1</math> и  <math>\angle 3</math> равны
+Треуг. ABD = треуг. BCD по 3м сторонам ( AB=CD, BC = AD, BD-общая)
+. Значит  <math>\angle 2</math> и  <math>\angle 4</math> равны , '''ч.т.д.'''