Теорема о двух секущих: различия между версиями
Перейти к навигации
Перейти к поиску
(Новая страница: «Файл:10 две секущих.jpg») |
|||
| Строка 1: | Строка 1: | ||
| + | ==Формулировка== | ||
| + | ''Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на ее внешнюю часть равно произведению другой секущей на ее внешнюю часть. '' | ||
| + | |||
| + | |||
[[Файл:10 две секущих.jpg]] | [[Файл:10 две секущих.jpg]] | ||
| + | |||
| + | |||
| + | ==Доказательство== | ||
| + | |||
| + | ∠1 - внешний угол для ΔCOD | ||
| + | ∠2 - внешний угол для ΔAOB | ||
| + | |||
| + | ∠2=∠COD+∠D | ||
| + | ∠1=∠AOD+∠B | ||
| + | ∠COD=∠AOD (как вертикальные) | ||
| + | ⇒∠D=∠B | ||
| + | |||
| + | ΔMAD∼ΔMCB | ||
| + | ⇒ MA/MD=MC/MB | ||
| + | MA*MB=MC*MD | ||
| + | |||
| + | '''ч.т.д.''' | ||
Текущая версия на 18:20, 8 февраля 2020
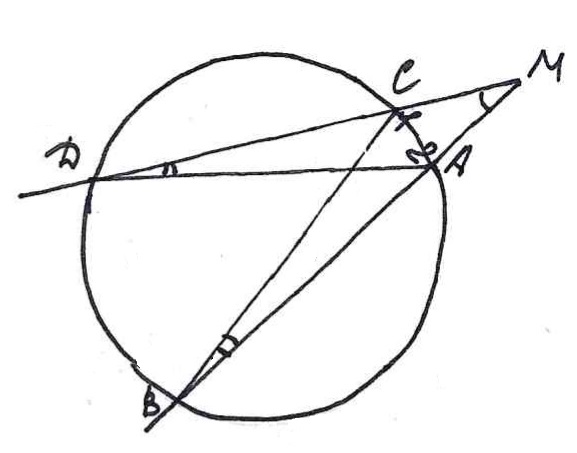
Формулировка
Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на ее внешнюю часть равно произведению другой секущей на ее внешнюю часть.
Доказательство
∠1 - внешний угол для ΔCOD ∠2 - внешний угол для ΔAOB ∠2=∠COD+∠D ∠1=∠AOD+∠B ∠COD=∠AOD (как вертикальные) ⇒∠D=∠B
ΔMAD∼ΔMCB ⇒ MA/MD=MC/MB MA*MB=MC*MD
ч.т.д.