Теорема о вписанном угле: различия между версиями

Материал из wiki.spbal.ru
Перейти к навигации Перейти к поиску
 
 
Строка 1: Строка 1:
 +
==Формулировка==
 +
''Вписанный угол равен половине дуги, на которую он опирается..''
 +
 +
 +
 +
==Доказательство==
 
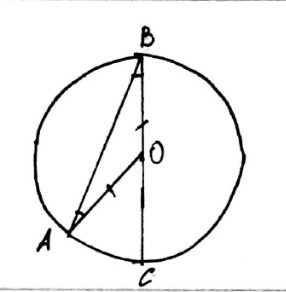
[[Файл:4 впис угол А.jpg]]
 
[[Файл:4 впис угол А.jpg]]
 +
 +
1.BO=АO=r ⇒ ΔAOB - равнобедренный
 +
⇒ <math>\angle A</math> = <math>\angle B</math>
 +
<math>\angle AOC</math> - внешний для  ΔAOB
 +
⇒ <math>\angle AOC</math>= <math>\angle B</math>+<math>\angle A</math>= 2 <math>\angle B</math>
 +
⇒ <math>\angle B</math> = 1/2 ∪ AC
 +
 +
 
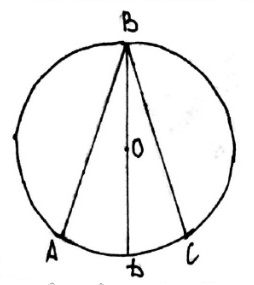
[[Файл:4 впис угол Б.jpg]]
 
[[Файл:4 впис угол Б.jpg]]
 +
 +
2. <math>\angle ABC</math>= <math>\angle ABD</math>+<math>\angle CBD</math>
 +
<math>\angle ABD </math> = 1/2 ∪ AD
 +
<math>\angle CBD </math> = 1/2 ∪ CD
 +
⇒ <math>\angle ABC</math> = 1/2 ∪ AD+1/2 ∪ CD = 1/2 ∪ AC
 +
 +
 
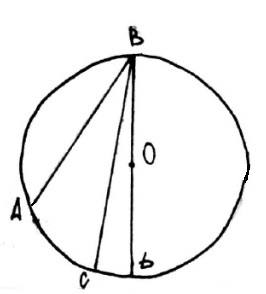
[[Файл:4 впис угол В.jpg]]
 
[[Файл:4 впис угол В.jpg]]
 +
 +
3.<math>\angle ABC</math>= <math>\angle ABD</math>-<math>\angle CBD</math>
 +
<math>\angle ABD </math> = 1/2 ∪ AD
 +
<math>\angle CBD </math> = 1/2 ∪ CD
 +
<math>\angle ABC</math> = 1/2 ∪ AD-1/2 ∪ CD = 1/2 ∪ AC

Текущая версия на 17:27, 8 февраля 2020

Формулировка

Вписанный угол равен половине дуги, на которую он опирается..


Доказательство

4 впис угол А.jpg 

1.BO=АO=r ⇒ ΔAOB - равнобедренный 
⇒  = 
 - внешний для  ΔAOB 
⇒ = += 2 
⇒  = 1/2 ∪ AC


4 впис угол Б.jpg 

2. = + 
 = 1/2 ∪ AD
 = 1/2 ∪ CD
⇒  = 1/2 ∪ AD+1/2 ∪ CD = 1/2 ∪ AC


4 впис угол В.jpg 

3.= -
 = 1/2 ∪ AD
 = 1/2 ∪ CD
 = 1/2 ∪ AD-1/2 ∪ CD = 1/2 ∪ AC
Источник — https://wiki.spbal.ru/index.php?title=Теорема_о_вписанном_угле&oldid=164