Теорема о вертикальных углах: различия между версиями
MV (обсуждение | вклад) |
|||
| (не показано 14 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | ==Формулировка== | |
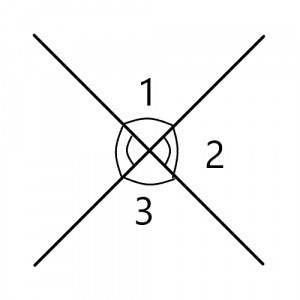
| + | [[Вертикальные углы]] равны | ||
| − | [[Файл: | + | [[Файл:vertical.png|thumb|Вертикальные углы]] |
| + | ==Доказательство== | ||
| − | < | + | 1. Углы <math>\angle 1</math> и <math>\angle 2</math> – смежные, значит <math>\angle 1 + \angle 2 = 180^\circ</math>. |
| − | + | 2. Углы <math>\angle 3</math> и <math>\angle 2</math> – смежные, значит <math>\angle 3 + \angle 2 = 180^\circ</math>. | |
| − | + | 3. <math>\angle 1 = 180^\circ -\angle 2</math> | |
| − | |||
| − | |||
<p>4. <math>\angle 3 = 180^\circ -\angle 2</math> | <p>4. <math>\angle 3 = 180^\circ -\angle 2</math> | ||
| − | <p>5. Значит, <math> \angle 1 = \angle 3 </math> | + | <p>5. Значит, <math> \angle 1 = \angle 3 </math>, '''ч.т.д.''' |
Текущая версия на 19:40, 9 февраля 2020
Формулировка
Вертикальные углы равны
Доказательство
1. Углы Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \angle 1} и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \angle 2} – смежные, значит Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \angle 1 + \angle 2 = 180^\circ} .
2. Углы Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \angle 3} и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \angle 2} – смежные, значит Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \angle 3 + \angle 2 = 180^\circ} .
3. Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \angle 1 = 180^\circ -\angle 2}
4. Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \angle 3 = 180^\circ -\angle 2}
5. Значит, Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \angle 1 = \angle 3 } , ч.т.д.