Теорема о вертикальных углах: различия между версиями

Текущая версия на 07:46, 7 мая 2024

Вертикальные углы

1. Углы $\angle 1$ и $\angle 2$ – смежные, значит $\angle 1+\angle 2=180^{\circ }$ .

2. Углы $\angle 3$ и $\angle 2$ – смежные, значит $\angle 3+\angle 2=180^{\circ }$ .

3. $\angle 1=180^{\circ }-\angle 2$

4. $\angle 3=180^{\circ }-\angle 2$

5. Значит, $\angle 1=\angle 3$ , ч.т.д.

@@ Строка 1: / Строка 1: @@
-<strong>Вертикальные углы равны</strong>
+==Формулировка==
+[[Вертикальные углы]] равны
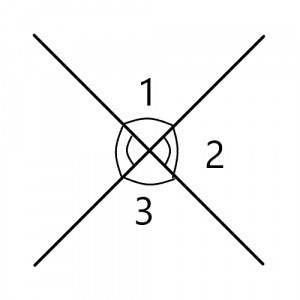
+[[Файл:vertical.png|thumb|Вертикальные углы]]
+==Доказательство==
+. Углы <math>\angle 1</math> и <math>\angle 2</math> &ndash; смежные, значит <math>\angle 1 + \angle  2 = 180^\circ</math>.
+. Углы <math>\angle 3</math> и <math>\angle 2</math> &ndash; смежные, значит <math>\angle 3 + \angle  2 = 180^\circ</math>.
-<p><u>Доказательство:</u>
-. Углы <math>\angle 1</math> и <math>\angle 2</math> -- смежные, и дают в сумме <math>180^\circ</math>.
-. Углы <math>\angle 3</math> и <math>\angle 2</math> -- смежные, и дают в сумме <math>180^\circ</math>.
 . <math>\angle 1 = 180^\circ -\angle 2</math>
-. <math>\angle 3 = 180^\circ -\angle 2</math>
-/ Значит, <math> \angle 1 = \angle 3 </math>
+<p>4. <math>\angle 3 = 180^\circ -\angle 2</math>
+<p>5. Значит, <math> \angle 1 = \angle 3 </math>, '''ч.т.д.'''